民立中学第一学期高二期中考试
数学试题
注意：考试时间120分钟，满分100分.
1、填空题（6*3+6*4=42分）
1.方程组
的增广矩阵是__________
2.若直线
的斜率没有，则直线的倾斜角
=__________
3.三阶行列式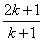
中，元素1的代数余子式的值是__________
4.已知平面内两点P、Q的坐标分别为（-2，4）、（2，1），则
的单位向量
=__________
5.计算：
__________
6.两平行直线x+y-2=0与2x+2y+1=0的距离是__________
7.在△ABC中，已知
为△ABC的重点，用表示向量
=__________
8.在无穷等比数列
中，若
，则首项
的取值范围是__________
9.经过点A（1，0）且一直线x-y+3=0成30°角的直线方程是__________
10.已知直线过点P（-1，2），且与以A（-2，-3），B（3，0）为端点的线段相交，则直线的斜率的取值范围是__________
11.设两点，则点P的坐标可表示为__________
12.△ABC中BC边上的高所在直线方程为x-2y+1=0，∠A平分线方程为y=0，顶点B的坐标为（1，2），则△ABC的面积为__________
2、选择题（4×4=16分）
13.假如过P（-2，m）,Q（m，4）两点的直线的斜率为1，那样m的值是（ ）
A.1 B.4 C.1或3 D.1或4
14.用数学总结法证明“
”时，从“n=k”到“n=k+1”坐边需要添加的代数式为（ ）
A. B. C.2k+1 D.2（2k+1）
15.已知
，则实数a的取值范围是（ ）
A.（-4，2） B.（-4，+∞） C.[-4，2] D.
16.设A（a，1），B（2，b）,C（4，5）为平面上三点，O是原点，若
方向上的投影相同，则a与b满足的关系式是（ ）
A.5a-4b=3 B.4a-5b=3 C.5a+4b=14 D.4a+5b=14
3、解答卷（8+10+10+14=42分）
17.△ABC中，已知A（-1，2），B（3，4），C（-2，5）
（1）求BC边所在的直线的一般式方程；
（2）求BC边上的高AH所在的直线的一般式方程.
18.用行列式解关于x、y的方程组：
，并对解的状况进行讨论.
19.已知平面山三个向量
的模均为1，它们互相之间的夹角为120°
（1）求证：
；
（2）若
，求k的取值范围.
20.如图☆的曲线，其生成办法是
（I）将正三角形【图（1）】的每边三等分，并以中间的那一条线段为一底边向形外作等边三角形，然后去掉底边，得到图；
将图的每边三等分，重复上述的作图办法，得到图；
再按上述办法继续做下去，所得到的曲线称为雪花曲线
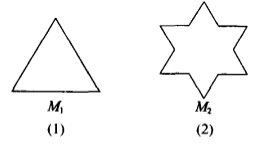
设图的等边三角形的边长为1，并且分别将图（1）、、…中的图形依次记作M1、M2、M3、…
…
设中的边数为
中每条边的长度为，写出数列和
的递推公式与通项公式；
设的周测为
，所围成的面积为，求数列{}与{}的通项公式；
请问周长与面积的极限是不是存在？若存在，求出该极限，若没有，简单说明理由.
